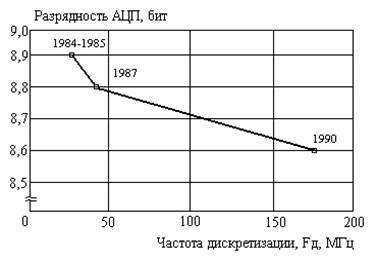
Основной тенденцией развития современных измерительных приборов — от цифровой осциллографии к анализаторам сигналов и далее к измерительным процессорам сигналов, реализующим концепцию замкнутых измерительных систем. В последних реализуется цифровой синтез тестовых сигналов и анализ отклика. При этом с 1984 по 1990 год наблюдалась устойчивая тенденция повышения частоты дискретизации за счет сокращения точности
Дискретизация и восстановление сигнала
Конкретное значение частоты дискретизации Fд определяется принятым в цифровом осциллографе способом восстановления аналогового сигнала (по его цифровым эквивалентам), целями и задачами восстановления и представления графической информации, структурой и погрешностями преобразования, требуемой окончательной погрешностью восстановления. Причины этого в неидеальности восстанавливающих фильтров ограниченности времени восстановления, в плохом или отсутствующем ограничении спектров исходных сигналов.
Наиболее прост точечный вывод, дающий удовлетворительный результат при малом расстоянии между точками (0,5-1,0 мм).
Также легко реализуется ступенчатая аппроксимация – восстанавливающий полином нулевой степени. Она дает значительные погрешности при малых разрешающих способностях по времени и амплитуде, особенно в режимах растяжки.
Наиболее распространен способ линейной (векторной) интерполяции полиномом первой степени.
Наиболее благоприятное и близкое к идеальному изображение при минимальной частоте дискретизации удается получить применением синусоидальной интерполяции. Этот метод реализуется с помощью цифрового фильтра нижних частот. Метод хорош при синусоидальных сигналах, но ухудшает восстановление сигналов импульсного характера. Хорошим выходом из положения является вариант двух методов с правом выбора предоставляемым оператору.
Погрешности восстановления
Чаще всего в цифровой осциллографии применяется равномерная дискретизация с шагом Tд=1/Fд.
Максимальное значение погрешности восстановления для случая ступенчатой аппроксимации:
[Δст(t)]макс=[Хст(t)-Х(t)]макс= (dx/dt)макс•Tд.
Для частного случая синусоидального сигнала
Fдмин≥[Um•ω•cos ωt]макс=Um•ω/Δ=Um•2ωf/Δ=2ωf/γ,
где γ- приведенная погрешность γ=Δ/Um.
Для синусоидального сигнала частотой 4 КГц при величине ошибки не более 1% требуется частота дискретизации 2,5 МГц, т.е. 600 отсчетов на один период частоты исследуемого сигнала.
При линейной интерполяции:
[Δл(t)]макс=[d² x/dt² ]макс•Тд/8.
Для того же примера требуется частота дискретизации 88 КГц, т.е. 20 отсчетов на периоде сигнала.
Результаты оценок показывают, что для восстановления сигналов при амплитудных измерениях с погрешностью 1-3% частота дискретизации для трех указанных методов должна превышать частоту исследуемого сигнала в 25, 15 и 2.5 раза соответственно.
Нормируемые характеристики
Чаще всего задаются следующие составляющие статической погрешности измерения амплитудных значений:
- Мультипликативная погрешность коэффициента отклонения по оси Y в виде предельного значения относительной погрешности (δм);
- Аддитивная погрешность квантования или разрешающая способность в виде предельного значения приведенной погрешности (γацп);
- Аддитивная погрешность смещения в виде предельного значения приведенной или абсолютной погрешности (γсм).
Общая погрешность определяется суммой составляющих.
Используются варианты нормирования погрешностей в виде двух составляющих: относительной погрешности аналогового канала и погрешности квантования.
Динамическая погрешность зависит от соотношения скорости изменения измеряемого сигнала и времени нарастания τн измерительного канала. Длительность фронта сигнала, измеренная на экране, связана с длительностью реального сигнала и временем нарастания измерительного канала:
τфэ ≈ √τф²+τн²
Иногда задается зависимость эффективного числа бит от частоты сигнала.
Совершенствование динамических характеристик
- Параллельная работа нескольких АЦП со сдвигом.
- Стробоскопическое преобразование
Оно реализуется в двух вариантах: по методу последовательно взятых отсчетов и методу случайных выборок. Во втором случае отсчет берется по ближайшему тактовому импульсу после сигнала синхронизации формируемого обычным путем в момент перехода сигнала через нуль. Интервал до тактового импульса измеряется интерполяционным методом (в цифровой форме).
Для повышения разрешающей способности широко используется усреднение.
Библиографический список
- Приборы, средства автоматизации и системы управления
ТС-5 «Средства электроизмерительной техники, геофизическая и гидрометеорологическая аппаратура»
Выпуск 1 - В.А. Панфилов. Современные цифровые осциллографы и анализаторы сигналов, их применение. Москва 1991 г.
